2️⃣

타원곡선

타원곡선의 유래

•
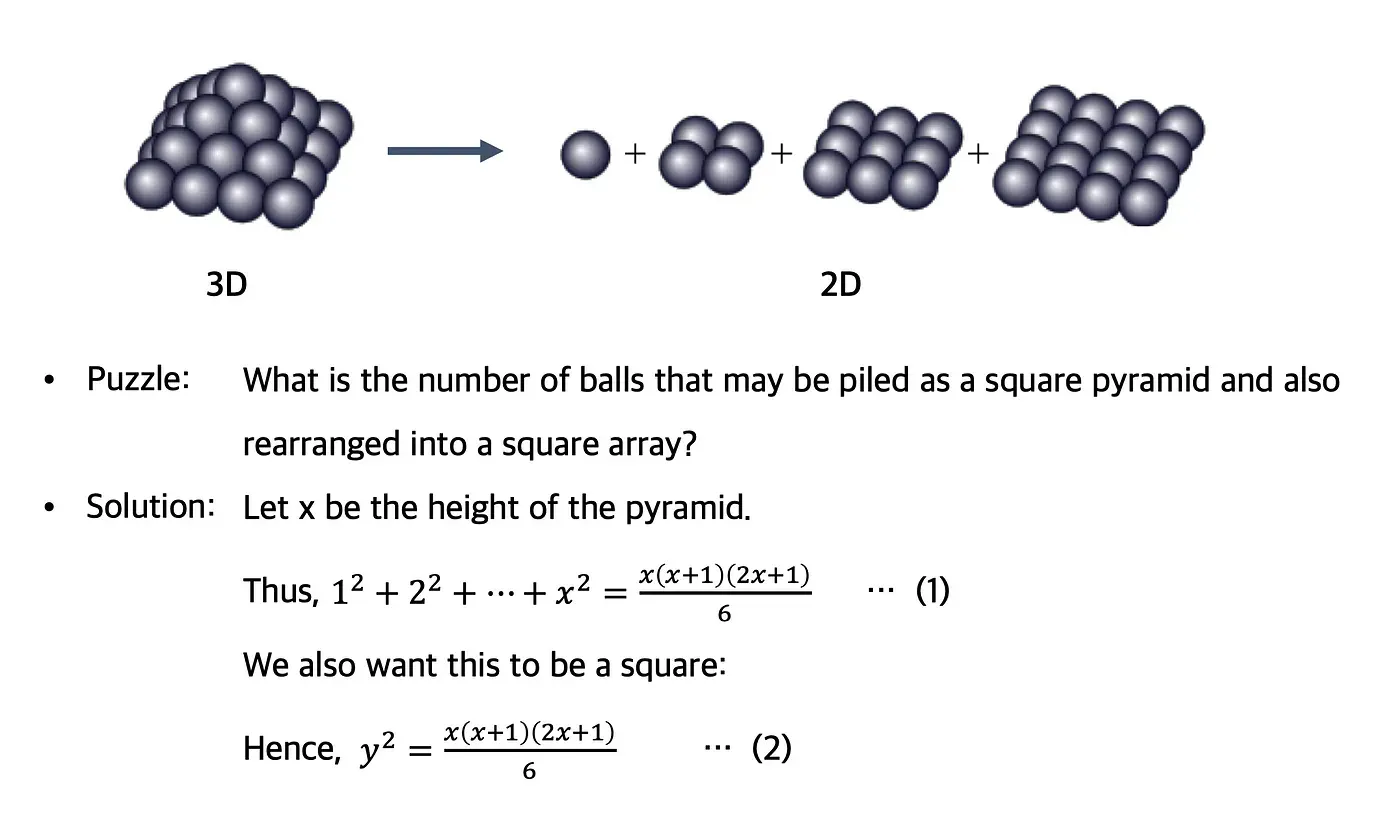
고대 그리스 수학자인 디오판토스가 낸 퍼즐에서 기원을 찾을 수 있다.
•
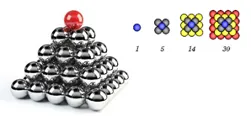
피라미드 쌓기 문제로 발견한 함수
•
탑의 높이를 x 라 할 때, 필요한 공의 수는 다음과 같다.
12+22+32+∼+x2{1}^{2}+{2}^{2}+{3}^{2}+\sim +{x}^{2}
•
자연수 거듭제곱의 합을 구하는 공식에 따라 다음처럼 유도가 가능하다.
y2=x(x+1)(2x+1)6{y}^{2}=\frac{x(x+1)(2x+1)}{6}
•
결국 이 함수는 다음과 형태를 갖는다.
•
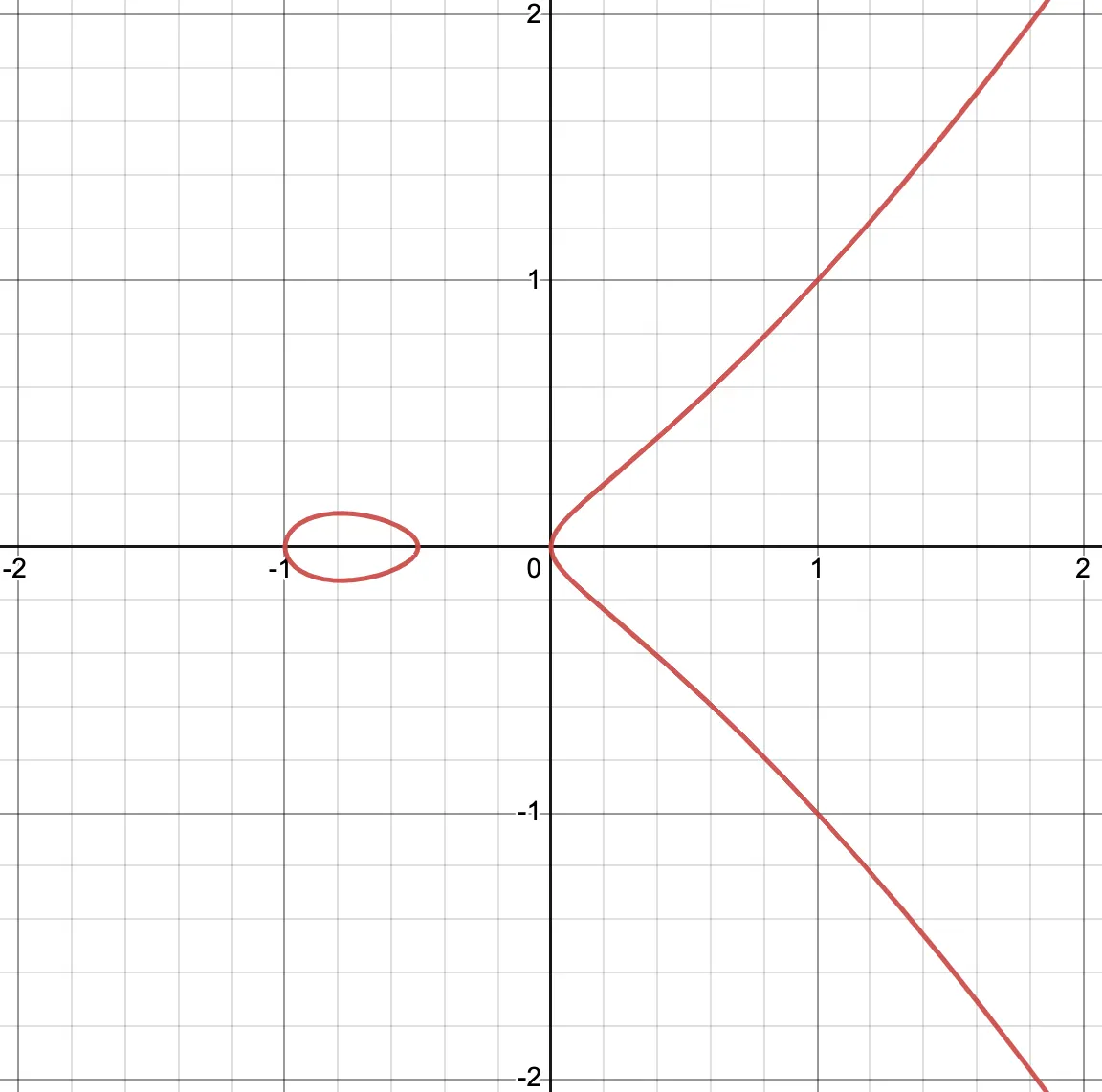
이 함수를 정리하면 다음과 같은 식의 형태를 얻을 수 있다. 이는 타원곡선 함수의 원형이 된다.
y2=x3+ax+b{y}^{2}={x}^{3}+ax+b
•
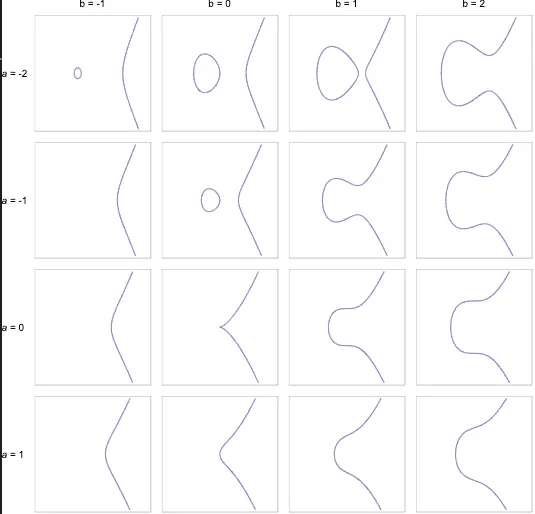
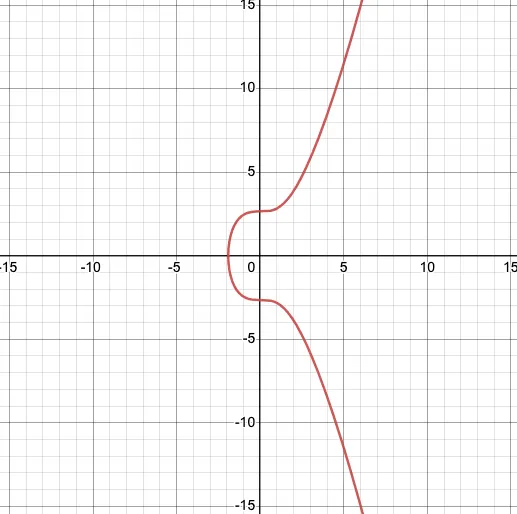
a, b 값에 따라 그래프의 모양은 아래와 같이 나타난다.
•
비트코인에서 사용하는 secp256k1은 타원곡선 함수를 다음과 같이 사용한다. (a=0, b=7)
y2=x3+7{y}^{2}={x}^{3}+7
타원 곡선 위의 점이 비트코인의 지갑에서 사용하는 공개키이다.

타원곡선의 덧셈

•
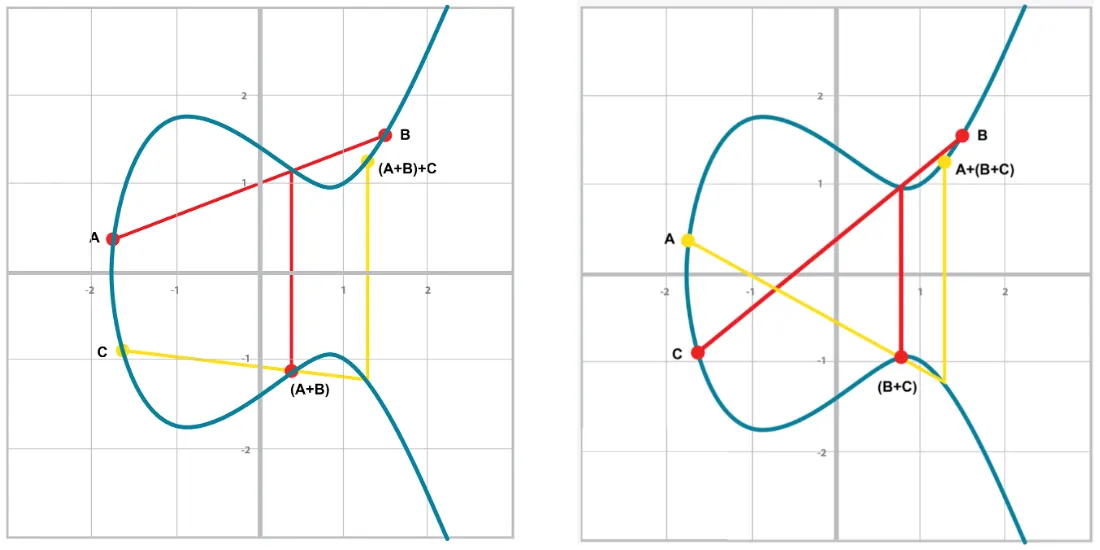
점 덧셈의 정의
◦
일반적인 덧셈 연산과는 다른 타원곡선 내의 두 점을 통해 연산하는 새로운 연산자이다.
◦
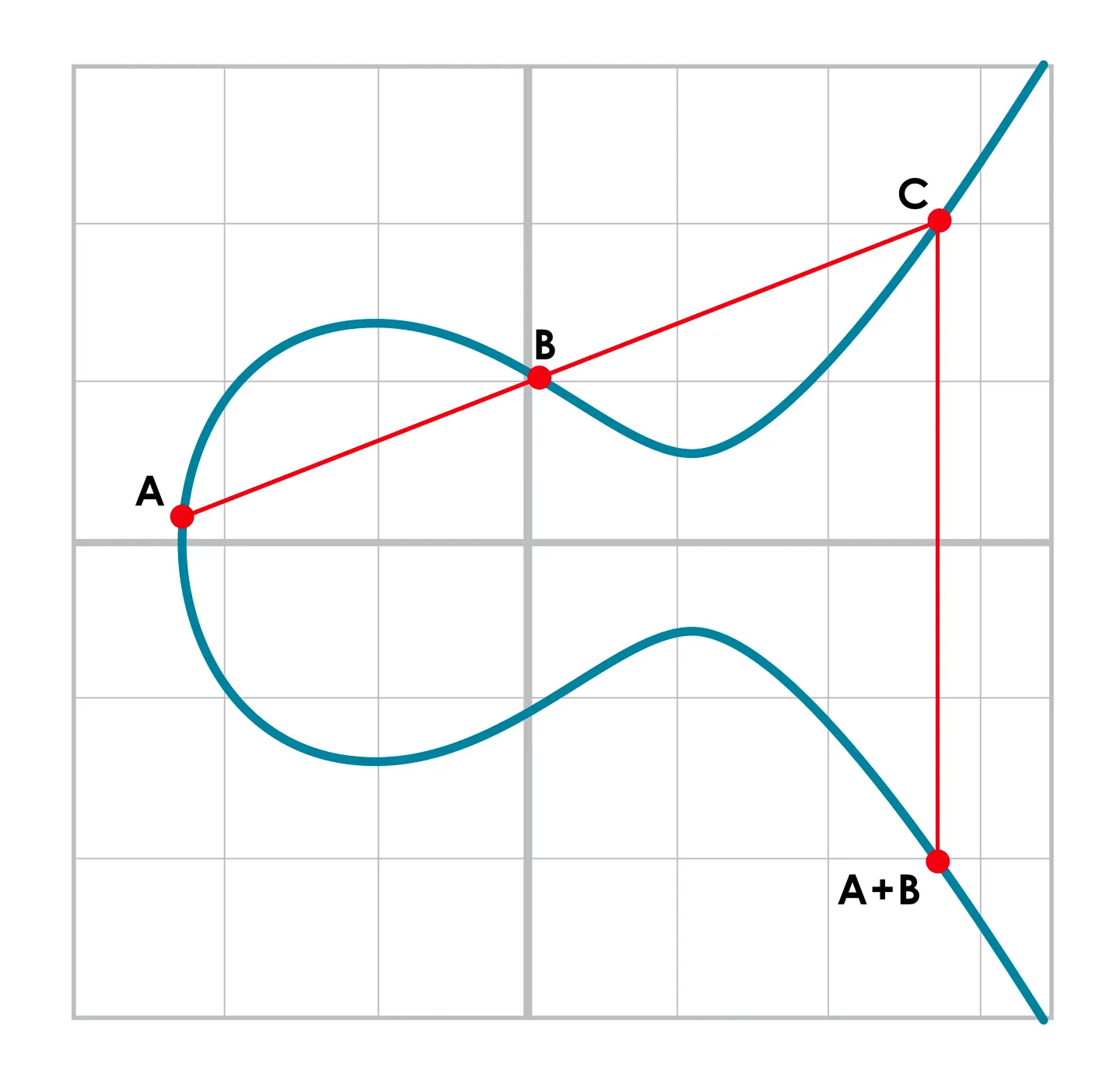
점 덧셈은 타원곡선의 두 점을 더해 제 3의 점을 얻는 과정을 말한다.
◦
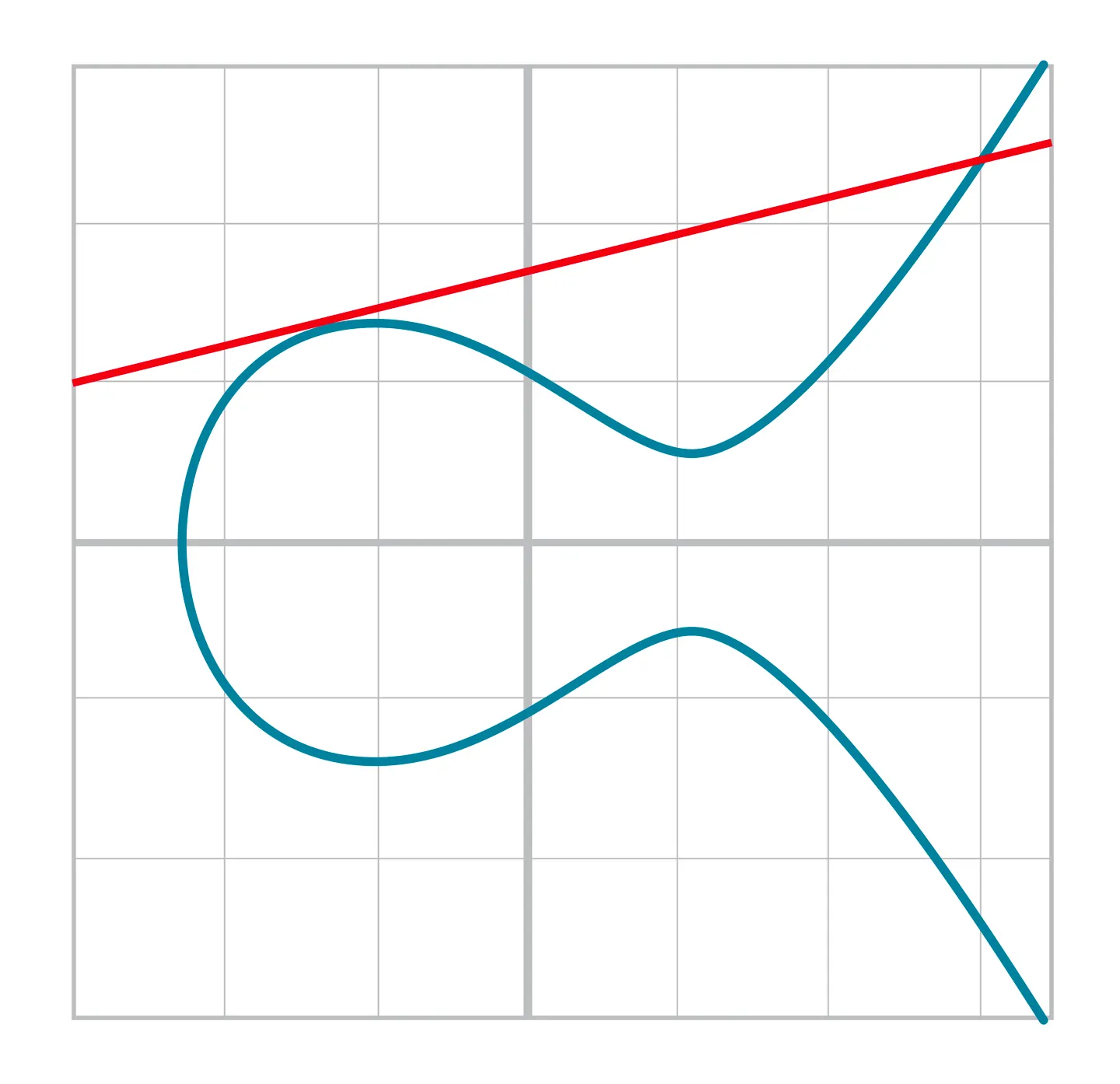
일부의 예외를 제외하고 어떤 직선이든 반드시 곡선의 점과 만난다.
◦
덧셈은 타원곡선의 두 점을 지나는 직선이 만나는 다른 접점을 x축으로 대칭시킨 점으로 정의한다.
◦
이 점 덧셈의 결과는 쉽게 예측하기 어렵다는 성질을 가진다.
•
점 덧셈의 성질
◦
항등원과 역원이 존재한다.
▪
더해도 자기 자신이되는 점을 무한원점(point at infinity)라 부른다.
▪
y축과 평행한 점이 그어져도 언젠간은 만날 수 있다는 것을 가정한다.
I+A=AI + A = A
▪
더해서 무한원점이 되는 점이 존재한다.
A+(−A)=IA + (-A) = I
▪
역원이 존재하므로 항등원이 존재할 수 있다.
▪
점 덧셈에서 항등원은 무한원점이다.
◦
교환법칙과 결합법칙의 성립
▪
점 덧셈은 순서과 관계 없으므로 자연스럽게 결합법칙이 성립한다.
A+B=B+AA+B = B+A
▪
교환법칙은 눈으로 직접 확인해볼 수 있다.
(A+B)+C=A+(B+C)(A+B)+C=A+(B+C)
•
점 덧셈의 공식
◦
다음 타원 곡선을 가정한다.
y2=x3+ax+b{y}^{2}={x}^{3}+ax+b
◦
세 개의 점을 정의해보자.
P1=(x1, y1), P2=(x2, y2), P3=(x3, y3)P3=P1+P2{P}_{1}=({x}_{1},~{y}_{1}),~{P}_{2}=({x}_{2},~{y}_{2}),~ {P}_{3}=({x}_{3},~{y}_{3})\\ {P}_{3}={P}_{1}+{P}_{2}
◦
더하는 두 점은 같은 직선에 있으므로 기울기와 y절편을 구할 수 있다.
s=(y2−y1)/(x2−x1)y=s(x−x1)+y1s=({y}_{2}-{y}_{1})/({x}_{2}-{x}_{1}) \\ y=s(x-{x}_{1})+{y}_{1}
◦
타원 방정식에 대입해보자.
y2=(s(x−x1)+y1)2=x3+ax+b{y}^{2}={(s(x-{x}_{1})+{y}_{1})}^{2}={x}^{3}+ax+b
◦
정리하면 다음과 같다.
x3−s2x2+(a+2s2x1−2sy1)x+b−s2x12+2sx1y1−y12=0   (A){x}^{3}-{s}^{2}{x}^{2}+(a+2{s}^{2}{x}_{1}-2s{y}_{1})x+b-{s}^{2}{{x}_{1}}^{2}+2s{x}_{1}{y}_{1}-{{y}_{1}}^{2}=0~~~(A)
◦
모든 x점은 윗 방정식을 만족하는 근이므로 다음과 같은 형식이어야 한다.
(x−x1)(x−x2)(x−x3)=0x3−(x1+x2+x3)x2+(x1x2+x1x3+x2x3)x−x1x2x3=0  (B)(x-{x}_{1})(x-{x}_{2})(x-{x}_{3})=0 \\ {x}^{3}-({x}_{1}+{x}_{2}+{x}_{3}){x}^{2}+({x}_{1}{x}_{2}+{x}_{1}{x}_{3}+{x}_{2}{x}_{3})x-{x}_{1}{x}_{2}{x}_{3}=0 ~~(B)\\
◦
(A), (B) 식을 근과 계수의 관계에 따라 같은 차수들의 계수는 동일해야 한다.
−s2=−(x1+x2+x3)-{s}^{2}=-({x}_{1}+{x}_{2}+{x}_{3})
◦
이를 통해 다음을 구할 수 있다.
x3=s2−x1−x2{x}_{3}={s}^{2}-{x}_{1}-{x}_{2}
◦
이를 직선의 방정식에 대입하여 도출 가능
y=s(x−x1)+y1 y=s(x-{x}_{1})+{y}_{1}
◦
y는 반대부호를 가져야 함.
y3=−(s(x3−x1)+y1)=s(x1−x3)−y1y_3=-(s(x_3-{x}_{1})+{y}_{1})=s(x_1-{x}_{3})-{y}_{1}
◦
공식 도출 완료
s=(y2−y1)/(x2−x1)x3=s2−x1−x2y3=s(x1−x3)−y1s=({y}_{2}-{y}_{1})/({x}_{2}-{x}_{1}) \\{x}_{3}={s}^{2}-{x}_{1}-{x}_{2} \\ y_3=s(x_1-{x}_{3})-{y}_{1}
덧셈의 결과(x,y) 를 얻기 위해서는 1. 두 점의 기울기를 먼저 구한다. 2. 기울기를 통해 x좌표를 구한다. 3. 기울기와 x좌표를 통해 y좌표를 구한다.
•
두 점이 같은 경우 점 덧셈 계산
◦
두 점이 같은 경우는 아래와 같다.
◦
다음 타원 곡선을 가정한다.
y2=x3+ax+b{y}^{2}={x}^{3}+ax+b
◦
두 개의 점을 정의해보자.
P1=(x1, y1), P3=(x3, y3)P3=P1+P1{P}_{1}=({x}_{1},~{y}_{1}),~ {P}_{3}=({x}_{3},~{y}_{3})\\ {P}_{3}={P}_{1}+{P}_{1}
◦
덧셈 유도 공식에 따라 아래 공식이 유도된다.
x3=s2−2x1y3=s(x1−x3)−y1{x}_{3}={s}^{2}-2{x}_{1} \\ y_3=s(x_1-{x}_{3})-{y}_{1}
◦
기울기를 구하기 위해서는 미분이 필요하다.
미분은 곡선에서 특정 점의 기울기를 구하는 데 활용한다. 기울기가 y의 증가량/x의 증가량 일 때, x의 증가량을 0으로 수렴하면 접선의 기울기를 구할 수 있다.
◦
순간 가속도(접점의 기울기)를 구하기 위해서는 다음을 구해야 한다.
dy/dxdy/dx
◦
타원곡선을 미분하면 다음과 같다.
2y dx=(3x2+a)dx2y~dx=(3x^2+a)dx
◦
정리하면 특정 x점에서 접선의 기울기를 구하는 공식은 다음과 같다.
dy/dx=(3x2+a)/(2y)dy/dx=(3x^2+a)/(2y)
◦
정리하면 기울기는 다음과 같다.
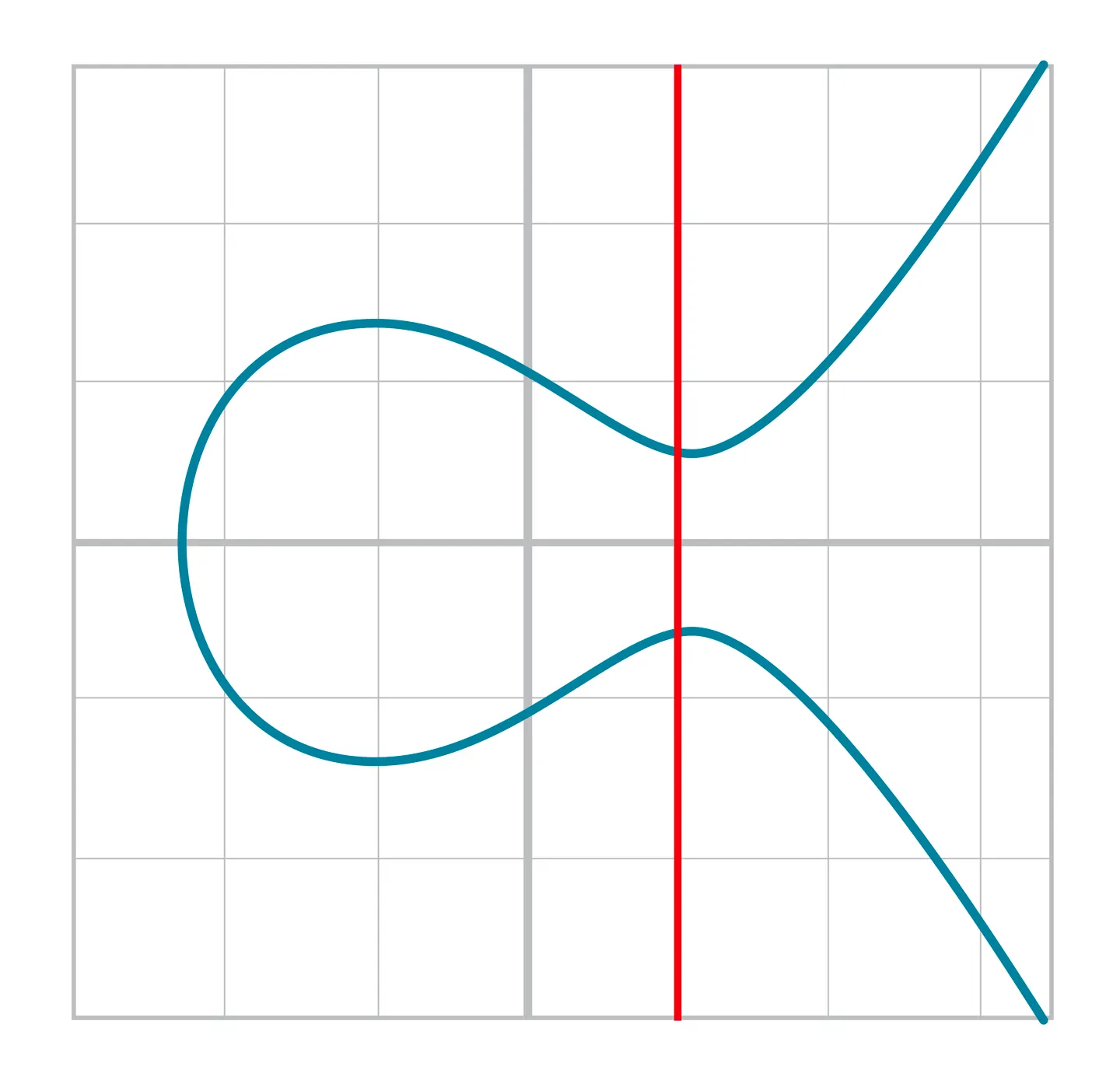
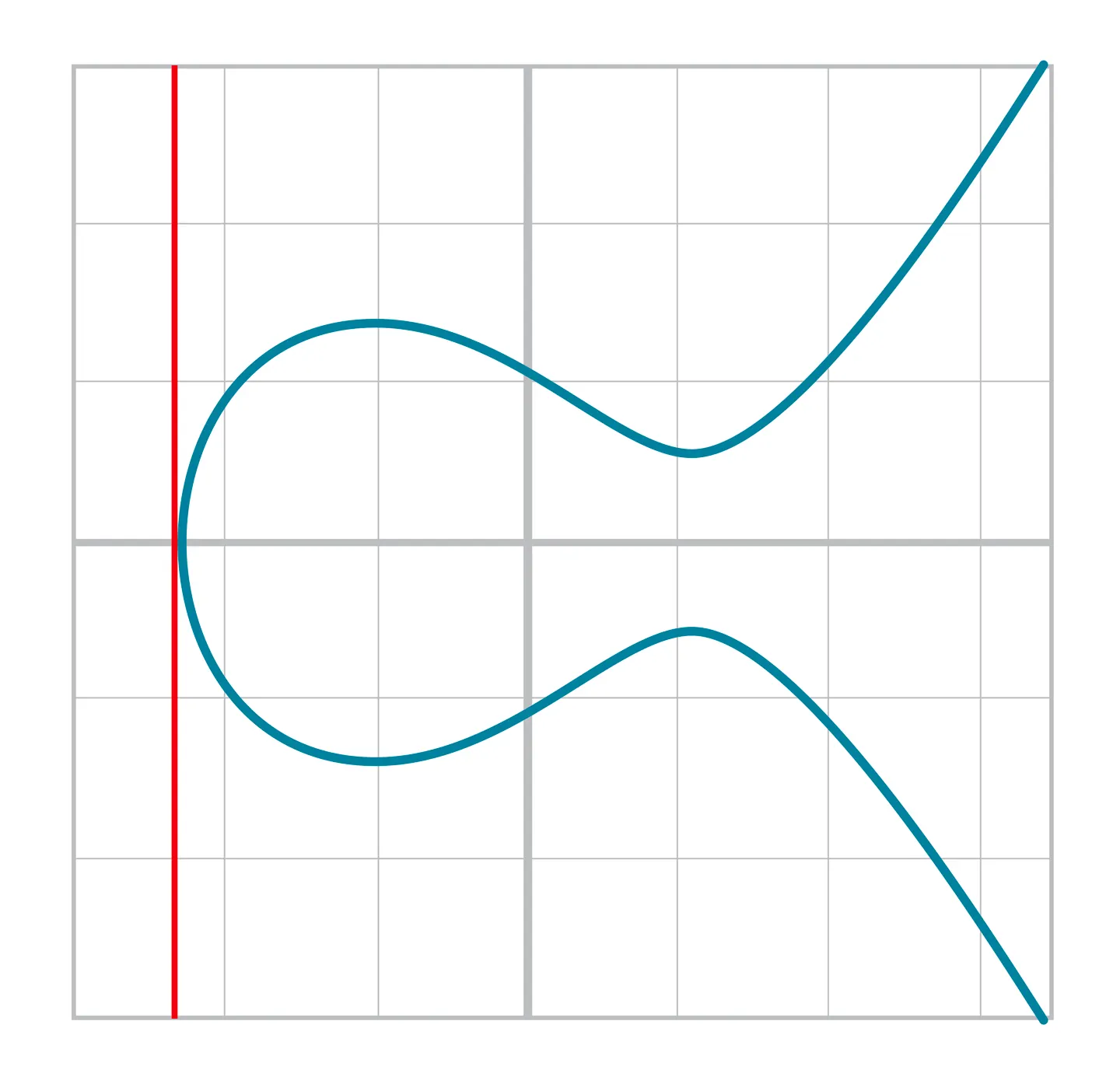
s=(3x12+a)/(2y1)x3=s2−2x1y3=s(x1−x3)−y1s=(3x_1^2+a)/(2y_1)\\{x}_{3}={s}^{2}-2{x}_{1} \\ y_3=s(x_1-{x}_{3})-{y}_{1}
•
직선이 y축과 평행인 경우
◦
아래와 같은 경우 만나는 점이 없으므로 덧셈이 불가능하다.
◦
이 경우는 무한원점을 반환하여야 한다.

구현: 타원곡선의 점

class Point: def __init__(self, x, y, a, b): self.a = a self.b = b self.x = x self.y = y if self.x is None and self.y is None: return if self.y**2 != self.x**3 + a * x + b: #x,y 두 점은 타원곡선 위에 있어야 한다. raise ValueError('({}, {}) is not on the curve'.format(x, y)) # end::source1[] def __eq__(self, other): return self.x == other.x and self.y == other.y \ and self.a == other.a and self.b == other.b def __ne__(self, other): # this should be the inverse of the == operator return not (self == other) def __repr__(self): if self.x is None: return 'Point(infinity)' elif isinstance(self.x, FieldElement): return 'Point({},{})_{}_{} FieldElement({})'.format( self.x.num, self.y.num, self.a.num, self.b.num, self.x.prime) else: return 'Point({},{})_{}_{}'.format(self.x, self.y, self.a, self.b) def __add__(self, other): #두 점의 타원곡선 함수가 다르면(두 점의 a,b가 다르면) 안된다. if self.a != other.a or self.b != other.b: raise TypeError('Points {}, {} are not on the same curve'.format(self, other)) #항등원 처리: 두 점중 하나가 무한원점이면 상대방 점을 리턴한다. if self.x is None: return other if other.x is None: return self #두 점의 x점이 같고 y점이 다른경우 (직선이 y축과 평행) if self.x == other.x and self.y != other.y: return self.__class__(None, None, self.a, self.b) #두 점이 같고, y값이 0인 경우 (직선이 y축과 평행) if self == other and self.y == 0 * self.x: return self.__class__(None, None, self.a, self.b) #두 점이 다른 경우 if self.x != other.x: s = (other.y - self.y) / (other.x - self.x) x = s**2 - self.x - other.x y = s * (self.x - x) - self.y return self.__class__(x, y, self.a, self.b) #두 점이 같은 경우 if self == other: s = (3 * self.x**2 + self.a) / (2 * self.y) x = s**2 - 2 * self.x y = s * (self.x - x) - self.y return self.__class__(x, y, self.a, self.b)
Python
복사
class PointTest(TestCase): def test_ne(self): a = Point(x=3, y=-7, a=5, b=7) b = Point(x=18, y=77, a=5, b=7) self.assertTrue(a != b) self.assertFalse(a != a) def test_on_curve(self): with self.assertRaises(ValueError): Point(x=-2, y=4, a=5, b=7) # these should not raise an error Point(x=3, y=-7, a=5, b=7) Point(x=18, y=77, a=5, b=7) def test_add0(self): a = Point(x=None, y=None, a=5, b=7) b = Point(x=2, y=5, a=5, b=7) c = Point(x=2, y=-5, a=5, b=7) self.assertEqual(a + b, b) self.assertEqual(b + a, b) self.assertEqual(b + c, a) def test_add1(self): a = Point(x=3, y=7, a=5, b=7) b = Point(x=-1, y=-1, a=5, b=7) self.assertEqual(a + b, Point(x=2, y=-5, a=5, b=7)) def test_add2(self): a = Point(x=-1, y=1, a=5, b=7) self.assertEqual(a + a, Point(x=18, y=-77, a=5, b=7))
Python
복사

참고자료