유한체의 타원곡선
•
앞에서 배운 타원곡선은 x, y값이 모든 실수에 해당된다.
•
이 함수에서 x값을 유한체로 한정할 수 있다.
•
점 덧셈을 위한 모든 연산은 유한체 연산을 적용한다.
•
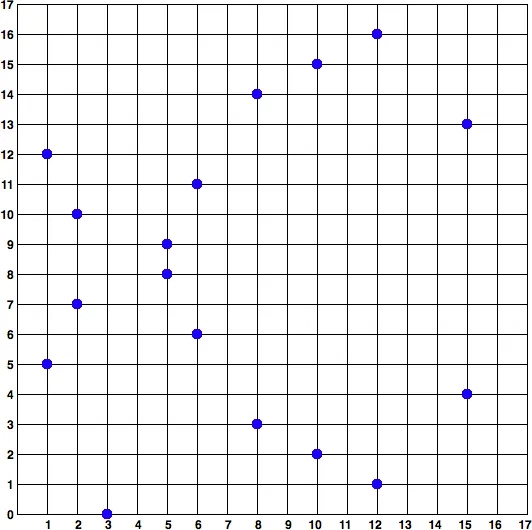
p(소수)가 17으로 정의된 아래의 타원 방정식을 정의해보자.
◦
x의 값은 자연수 0~16까지로 정의된다.
◦
모든 연산은 유한체의 연산이 적용된다.
◦
(5, 8)가 타원곡선에 있는가?
◦
이러한 방식으로 좌표를 나타내면 아래와 같다.
유한체 타원곡선의 덧셈
•
추출한 타원 곡선의 덧셈 공식에 유한체 연산을 적용해야 한다.
◦
예) 두 점이 다른 경우 (47,71) + (17,56), p=223
연산이 복잡해지기 때문에 손으로 따라가는 것은 쉽지 않다.
파이썬 코드를 통해 계산해보자.
▪
적용 공식은 다음과 같다.
▪
유한체 연산을 통해 구하기
from ecc import FieldElement
prime=223
a=FieldElement(0, prime)
b=FieldElement(7, prime)
x1=FieldElement(47,prime)
y1=FieldElement(71,prime)
x2=FieldElement(17,prime)
y2=FieldElement(56,prime)
s=((y2-y1)/(x2-x1))
x3=s**2-x1-x2
y3=s*(x1-x3)-y1
print("s=",s)
print("x3=",x3)
print("y3=",y3)
Python
복사
▪
포인트 연산을 통해 구하기
from ecc import Point
p1 = Point(FieldElement(47, prime), FieldElement(71, prime), a, b)
p2 = Point(FieldElement(17, prime), FieldElement(56, prime), a, b)
print(p1+p2)
Python
복사
▪
덧셈의 결과는 다음과 같다.
Point(215,68)_0_7 FieldElement(223)
Python
복사
타원곡선의 스칼라 곱셈
•
유한체가 결합법칙이 성립함에 따라 다음과 같이 곱셈으로도 표현이 가능하다.
•
이러한 방식의 곱셈을 스칼라 곱셈(scalar multiplication)이라 한다.
•
스칼라 곱셈은 실제 계산하지 않고는 예측이 대단히 어렵다. (이산로그 문제)
이산로그문제 (discrete logarithm problem)
•
아래의 수에서 만족하는 x를 구하는 것은 불가능하다.
•
거듭제곱의 역함수를 구하는 것은 불가능하다는 것에서 나온 문제이다.
•
가장 대표적인 이산로그 문제는 트랩도어 함수(trapdoor function)이다.
•
트랩도어 함수는 두 개의 큰 소수를 곱하는 것은 쉬우나 소인수분해는 어렵다는 점을 이용한다.
•
예를들어 8,018,009이 두 개의 소수(2003, 4003)의 곱으로 이루어졌다는 사실실을 밝히는 것은 어렵다.
•
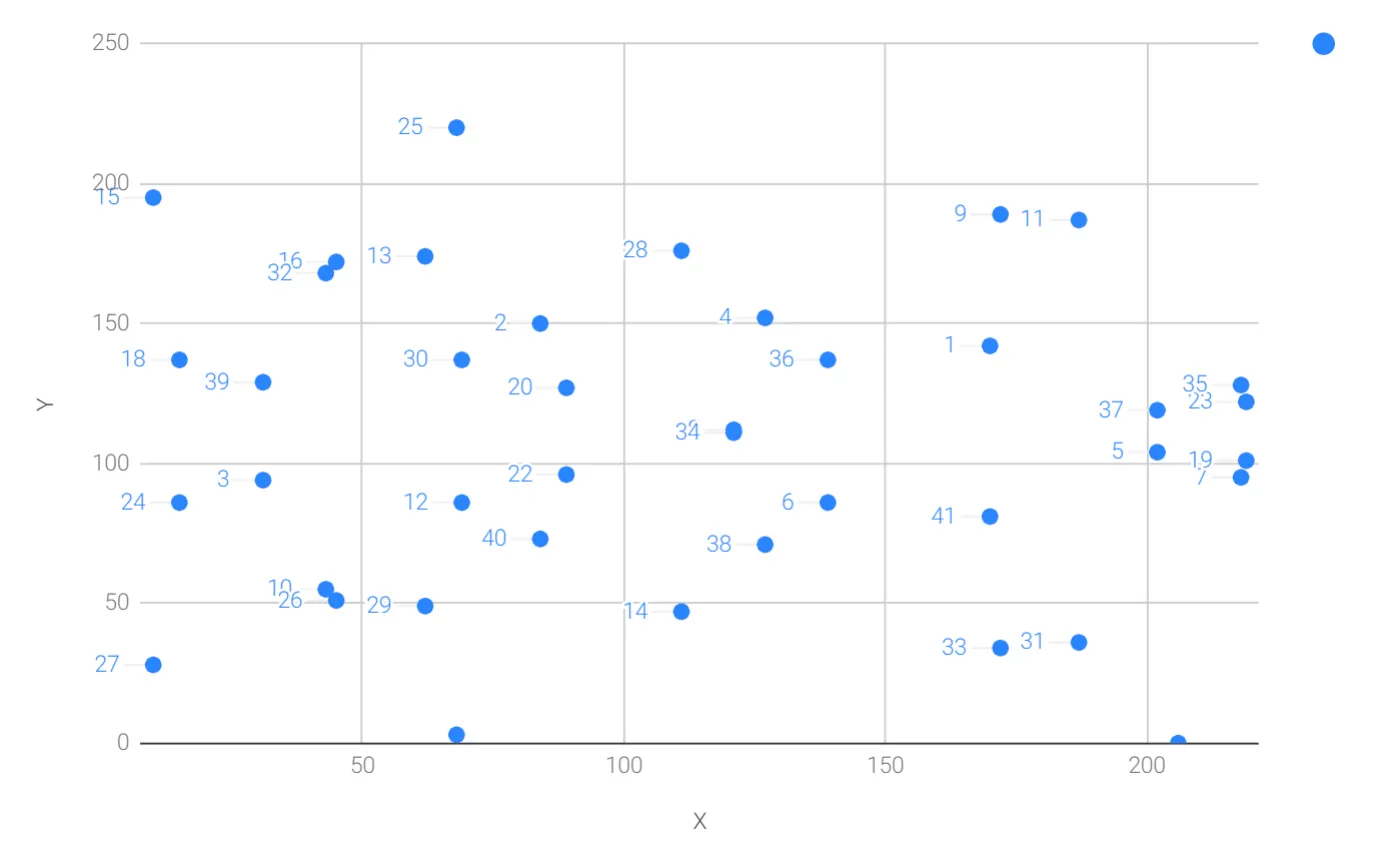
다음 그림은 p=223, (170,142)점에서 스칼라 곱셈의 결과를 나타낸다.
•
스칼라 곱셈은 지속적으로 곱하다 보면 언젠간 무한원점이 나타난다는 특징을 가진다.
•
따라서 다음과 같은 집합이 가능하다.
스칼라 곱셈과 유한순환군
•
스칼라 곱셈의 결과는 규칙적이지 않기 때문에 이산로그 문제에 해당된다.
•
아래는 p=223, (47,71)의 스칼라곱의 결과이다.
from ecc import FieldElement, Point
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
x = FieldElement(47, prime)
y = FieldElement(71, prime)
p = Point(x, y, a, b)
for s in range(1,21):
result = s*p
print('{}*(47,71)=({},{})'.format(s,result.x.num,result.y.num))
#-----결과-----
1*(47,71)=(47,71)
2*(47,71)=(36,111)
3*(47,71)=(15,137)
4*(47,71)=(194,51)
5*(47,71)=(126,96)
6*(47,71)=(139,137)
7*(47,71)=(92,47)
8*(47,71)=(116,55)
9*(47,71)=(69,86)
10*(47,71)=(154,150)
11*(47,71)=(154,73)
12*(47,71)=(69,137)
13*(47,71)=(116,168)
14*(47,71)=(92,176)
15*(47,71)=(139,86)
16*(47,71)=(126,127)
17*(47,71)=(194,172)
18*(47,71)=(15,86)
19*(47,71)=(36,112)
20*(47,71)=(47,152)
Python
복사
•
21을 곱하면 무한 원점이 되며, 22를 곱하면 다시 처음 점(41, 71)으로 돌아온다.
from ecc import FieldElement, Point
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
x = FieldElement(47, prime)
y = FieldElement(71, prime)
p = Point(x, y, a, b)
result = 22*p
print('{}*(47,71)=({},{})'.format(22,x.num,result.y.num))
#-----결과-----
22*(47,71)=(47,71)
Python
복사
•
한 점에서 무한원점(항등원)을 곱하면 자기 자신이 되므로 스칼라 곱셈의 결과는 순환한다.
•
이를 다른말로 유한순환군이라 한다.
•
유한순환군의 원소의 수를 위수라 한다.
구현: 스칼라 곱셈
class Point:
#Point 클래스에 곱셈 함수를 정의한다.
def __rmul__(self, coefficient):
coef = coefficient
current = self
#result를 무한원점으로 초기화 한다.
result = self.__class__(None, None, self.a, self.b)
#단순한 덧셈 누적인 경우 coefficient가 커지면 연산이 너무 오래 걸린다.
#결합법칙을 이용한다.
#A+A+A+A와 2(2A)가 같다는 점을 차용한다.
while coef:
#홀수인 경우 값을 한번 더 더한다.
if coef & 1:
result += current
#곱하기 2를 한다.
current += current
#비트연산을 통해 coef를 절반으로 낮춘다.
coef >>= 1
return result
#너무 이해가 어려우면 다음 함수로 이해해도 된다.
def __rmul__(self, coefficient):
product = self.__class__(None, None, self.a, self.b)
for _ in range(coefficient):
product += self
return produc
Python
복사